guglmet.blogg.se

• #TOWERS OF HANOI TOWERS OF HANOI TRIAL#

Notice that the steps highlighted in red are a step by step solution to the puzzle. The first shows which disks are being moved by each TOH function. To this end, I have included 2 tree diagrams (Click these diagrams to enlarge them). In my opinion, the best way to visualise this recursion is by trying an example. This repeated calling of a function within itself is a feature that is common to any kind of recursive method. These TOH functions with \( (N-1) \) disks as arguments will themselves call TOH functions with \( (N-2) \) disks and so on until TOH is called with \( 0 \) disks as an argument and the function STOPS. Notice how this is achieved in this function by executing TOH within TOH with \( (N-1) \) disks being moved from A to B via C then moving A to C and then executing TOH again with \( (N-1) \) disks being moved from B to C via A.

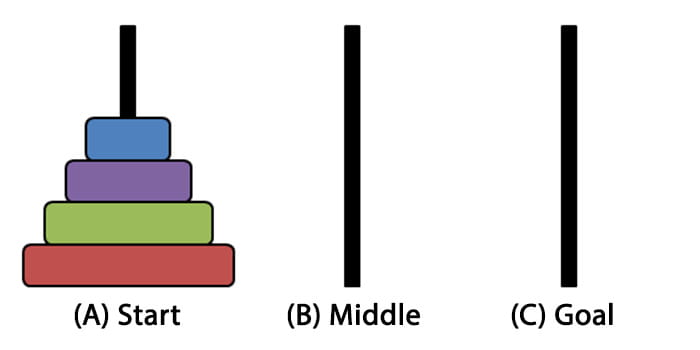
As I mentioned earlier, this can be decomposed into the problem of moving the \( (N-1) \) smaller disks from A to B then moving the largest disk from A to C and then moving the \( (N-1) \) smaller disks from B to C.

In this case, the first function wants to move \( N \) disks from rod A to rod C via rod B. The function TOH takes four arguments the first is the number of disks being moved, \( N \), and the next three arguments indicate the rod being moved from, the intermediate rod and the rod being moved to respectively. This means that we can break the problem down into the subproblems of moving \( (N-1) \) disks from A to B, moving A to C (which is trivial) and then moving \( (N-1) \) from B to C. The solutions of the subproblems are then collected together to give the solution to the larger problem.įor the tower of Hanoi problem, the important thing to realise is that because of how the puzzle works, at some stage we will have the situation shown below where \(\) (N-1) \) disks are on rod B and we have to move the largest disk from A to C and then all of the remaining disks from B to C. The philosophy behind solving problems using recursion is that we break a large problem down into sub-problems which can be solved using the same procedure in a simpler way.

#TOWERS OF HANOI TOWERS OF HANOI TRIAL#

It’s a relatively simple task, with a little trial and error, to solve this puzzle for the three-disk problem shown here but what if there are more disks? Is there some kind of rule we can come up with to be able to solve this no matter the number of disks, \( N, present? The answer is yes, kind of … In that we can find these rules by leveraging a programming/problem solving concept known as recursion but as I’ll explain later there is something else that limits our ability to solve the problem for large numbers of disks.